Hypothesis and Cost

*cost function - mse(mean square error)
Simplified hypothesis

*설명을 위해 b를 생략 (간략화)
What cost(W) looks like?
| X | Y |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
· W=1, cost(W)=0
1/3((1*1-1)^2+(1*2-2)^2+(1*3-3)^2)
· W=0, cost(W)=4.67
1/3((0*1-1)^2+(0*2-2)^2+(0*3-3)^2)
· W=2, cost(W)= ?
What cost(W) looks like?
· W=1, cost(W)=0
· W=0, cost(W)=4.67
· W=2, cost(W)=4.67
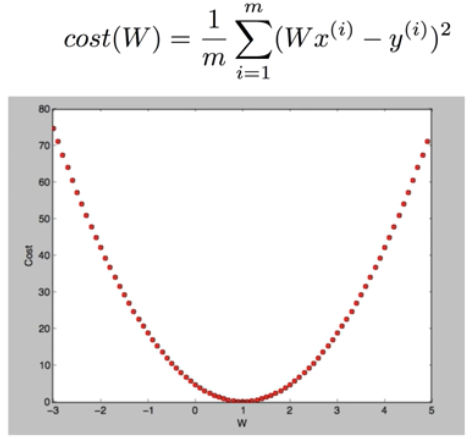
-목표는 cost가 최소화 되는 지점(W)를 기계적으로 찾는 것이다. 그 지점을 찾는 알고리즘을 Gradient descent algorithm이라고 한다.
Gradient descent algorithm (경사 하강법)
· Minimize cost function
· Gradient descent is used many minimization problems
· For a given cost function, cost(W, b), it will find W, b to minimize cost
· It can be applied to more general function : cost(w1, w2, .. )
How it works?
-How would you find the lowest point?
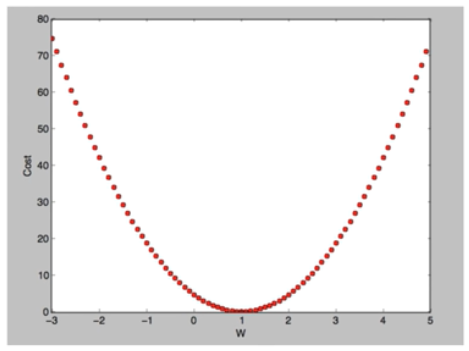
· Start with inital guesses
-Start at 0,0 (or any other value)
-Keeping changing W and b a little bit to try and reduce cost(W, b)
· Each time you change the parameters, you select the gradient which reduces cost(W, b) the most possible
· Repeat
· Do so until you converge to a local minimum
· Has an interesting property
-Where you start can determine which minimum you end up
시작점을 어디든 두더라도 cost를 minimize하는 방향으로 가기 위해서는 기울기가 필요하다. 수학에서는 기울기를 미분으로 구한다. 즉, 기울기를 구하기 위해서는 미분이 필요하다.
Formal definition

* 알파 : learning rate
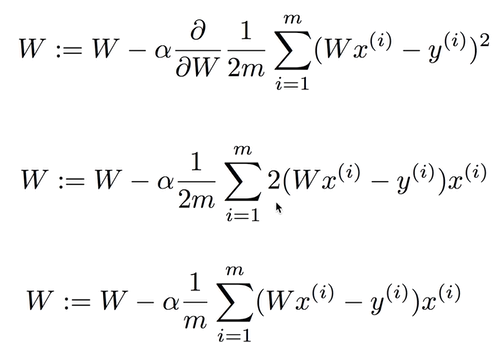
Convex function

우리가 배운 cost function을 3차원화했을 때 다음과 같은 형태의 모양을 갖게 된다. 어느 점에서 시작하더라도 결과는 하나의 점에서 만나게 된다. (global minimum)

하지만 cost function의 다른 형태에 따라서 다른 문제가 발생한다. 이 그림에서 문제점을 볼 수 있다. 다른 시작점에서 시작하는 두점이 cost를 minimize화를 거쳤을 때, 서로 다른 local에 빠지게 되는 문제점이 있다.
'Deep Learning lecture' 카테고리의 다른 글
| ML lec 04 - multi-variable linear regression (*new) (0) | 2020.04.27 |
|---|---|
| ML lab 03 - Linear Regression 의 cost 최소화의 TensorFlow 구현 (new) (0) | 2020.04.27 |
| ML lec 02 - TensorFlow로 간단한 Linear regression을 구현 (0) | 2020.04.25 |
| ML lec 02 - Linear Regression의 Hypothesis와 Cost 설명 (0) | 2020.04.25 |
| 모두를 위한 딥러닝 강좌 (0) | 2020.04.25 |



댓글