반응형
Predicting exam score : Regression
| x(hours) | y(score) |
| 10 | 90 |
| 9 | 80 |
| 3 | 50 |
| 2 | 30 |
데이터를 가지고 학습을 시킨다. (training) 학습을 통해 모델을 만들게 된다. 그리고 어떤 학생의 학습시간에 따라 몇점을 받을 수 있는지 예측하는 것이다.
ex) 어떤 학생이 7시간을 공부했다면 몇점정도 예상되는가? 65점...
Regression (presentation)

(Linear) Hypothesis

데이터에 따른 Linear한 Line을 찾는 것이 결국 학습하는 것이다.
Which hypothesis is better?

Hypothesis는 H(x) = Wx + b 라는 1차 방정식으로 표현할 수 있다. 중요한 것은 어떤 Line이 우리가 가지고 있는 Data에 적합한지를 찾아야 한다. (H(x)= 0.5x+2, H(x)=1x+0, H(x)=0.5x-1)
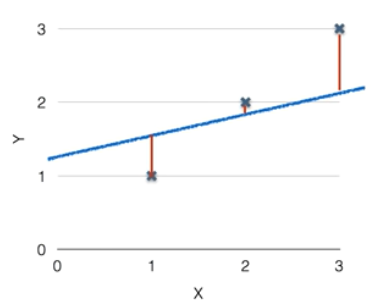
실제 Data와 Hypothesis위에 점의 거리를 계산한다. 이것을 Linaer Regression에서 Cost function 또는 Loss function이라고 부흔다.
Cost function
-How fit the line to our (training) data
보통 거리를 알아야 하기때문에 차이에 대에서 제곱을 해어 양수화 시킨다. (H(x) - y)^2

(m = data 갯수)

cost function은 w와 b의 function이 된다. 여기서 Linear Regression의 숙제는 cost를 minimize하는 것이다. 즉, 가장 작은 값을 가지는 w와 b를 구하는 것이다. 이것이 Linear Regression의 학습이 된다.
반응형
'Deep Learning lecture' 카테고리의 다른 글
| ML lec 04 - multi-variable linear regression (*new) (0) | 2020.04.27 |
|---|---|
| ML lab 03 - Linear Regression 의 cost 최소화의 TensorFlow 구현 (new) (0) | 2020.04.27 |
| ML lec 03 - Linear Regression의 cost 최소화 알고리즘의 원리 설명 (0) | 2020.04.26 |
| ML lec 02 - TensorFlow로 간단한 Linear regression을 구현 (0) | 2020.04.25 |
| 모두를 위한 딥러닝 강좌 (0) | 2020.04.25 |


댓글